Romer-Taylormodel

Het Romer-Taylormodel is een theoretisch model dat de oorzaken van conjunctuur gaat verklaren.
Het model werd gecreëerd door Paul Romer en John Taylor, twee economen die expert zijn op het gebied van economische groei en internationaal economisch beleid.
De geaggregeerde vraag[bewerken]
De geaggregeerde vraag is het geheel van goederen en diensten dat wordt gevraagd door de gezinnen, de ondernemingen, de overheid en het buitenland bij het algemeen prijspijl. Omdat de geaggregeerde vraag vooral zal reageren op veranderingen in het algemeen prijspeil geeft de geaggregeerde vraag in het Romer-Taylormodel de relatie weer tussen het reële bbp (Y) en het inflatiepeil.
Afleiden van de AD-curve[bewerken]
Het afleiden van de AD-curve verloopt in drie stappen.
Relatie reële rentevoet en het reële bbp[bewerken]
De reële rentevoet is de rentevoet die van toepassing is op beleggingen of op leningen die je aangaat. Bij een hoge reële rentevoet wordt geld lenen duurder. Ondernemingen zullen minder investeren omdat kosten hoger zijn. Ook gezinnen lenen en consumeren minder. Bij een lage reële rentevoet wordt lenen goedkoper. Ondernemingen investeren meer omdat de kosten lager zijn. Ook gezinnen lenen en consumeren meer.
Er is dus een negatief verband tussen de reële rentevoet (r) en het reële bbp (Y).

Relatie reële rentevoet en inflatie[bewerken]
De centrale bank streeft een inflatie van 2% na. De centrale bank kan de inflatie gaan bespelen door de reële rentevoet te doen stijgen of dalen. Bij een toenemende inflatie zal de centrale bank de reële rentevoet doen stijgen. Bij een afnemende inflatie zal de centrale bank de reële rentevoet doe afnemen.
Er is dus een positief verband tussen de reële rentevoet en het inflatiepeil.

AD-curve[bewerken]
Er is een positief verband tussen inflatiepeil en de reële rentevoet en een negatief verband tussen de reële rentevoet en het reële bbp. Hieruit volgt dus een negatief verband tussen het inflatiepeil en het reële bbp.
Als de inflatie versnelt doet de centrale bank de reële rentevoet stijgen. Deze rentevoet zorgt voor een daling van de vraag naar goederen en diensten.
Het negatieve verband tussen het inflatiepeil en het reële bbp wordt voorgesteld door de AD-Curve.

Verschuivingen van de AD-curve[bewerken]
Bij een stabiele inflatie kunnen er 4 factoren een invloed hebben op de totale hoeveelheid gevraagde goederen en diensten. Een toename van de geaggregeerde vraag leidt tot een verschuiving van de AD-curve naar rechts. Een afname naar links.
Verschuiving door consumptie[bewerken]
Verschuiving door investeringen[bewerken]
Verschuiving door overheidsuitgaven[bewerken]
Verschuiving door netto-export[bewerken]
Het inflatiepeil[bewerken]
Een tweede variabele in het Romer-Taylormodel is het inflatiepeil. Veranderingen in het prijspeil komen op korte termijn zelden voor. Dit komt enerzijds doordat inflatie grotendeels afhankelijk is van loonevolutie (worden op lange termijn onderhandeld), en anderzijds door een zekere prijsrigiditeit door ondernemingen.
Door deze twee veronderstellingen kunnen we vaststellen dat het inflatiepeil op korte termijn constant is ten opzichte van elk niveau van het reële bbp. Grafisch stellen we dit voor door een evenwijdige curve met de horizontale as, de IA-curve.
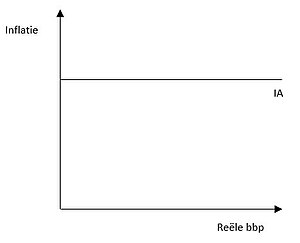
Het AD-IA diagram[bewerken]
Het snijpunt van de AD-curve met de IA-curve is het huidig niveau van het reële bbp bij het huidige inflatiepeil. Dit is het kortetermijnevenwicht (Y0).

In het kortetermijnevenwicht kan het reële bbp groter of kleiner zijn dan het potentiële bbp (Y*).
Langetermijnevenwicht bij het Romer-Taylormodel[bewerken]
Als het huidig niveau van het reële bbp (Y0) gelijk is aan het potentiële bbp (Y*), dan spreken we van een langetermijnevenwicht.

Herstel van het langetermijnevenwicht bij het Romer-Taylormodel[bewerken]
Als bij huidige inflatiepeil het reële bbp niet gelijk is aan het potentiële bbp, dan is er geen langetermijnevenwicht in de economie. Veranderingen in het inflatiepeil herstellen het evenwicht.

Dit artikel "Romer-Taylormodel" is uit Wikipedia. De lijst van zijn auteurs is te zien in zijn historische en/of op de pagina Edithistory:Romer-Taylormodel.
