Labyrint (wiskunde)

Naast het recreatieve en culturele aspect kan een labyrint worden gezien als wiskundig object. Labyrinten moeten niet verward worden met doolhoven: labyrinten bestaan uit een onvertakt pad dat zich niet snijdt.

Wiskundige structuur[bewerken]

Wendingen[bewerken]

In een labyrint zitten wendingen. Zo een wending is het overgangspunt tussen linksom draaiend en rechtsom draaiend. Bij de structuur van een labyrint houden we geen rekening met de metrische eigenschappen zoals de lengte en de oppervlakte. Ook met de vorm houden we geen rekening. Wel kijkt men bij een labyrint naar het aantal wendingen.

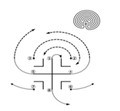
Cirkelvormig Kreta labyrint met 8 wendingen
Vierkantige Kreta labyrint met 8 wendingen

Niveaus[bewerken]

Een labyrint kan je vergelijken met een appartementsgebouw: het bestaat uit verschillende verdiepingen. Bij labyrinten praten we echter niet over verdiepingen maar over niveaus. Het aantal niveaus van een labyrint is heel gemakkelijk te bepalen door een rechte lijn te tekenen van het doel (middelpunt van labyrint) naar het buitenste deel van het labyrint waarbij de lijn zo vaak mogelijk het pad snijdt.

Niveaurij[bewerken]

De rij van getallen die de volgorde waarin de niveaus worden doorgelopen weergeeft als je van niveau 0 tot het doel gaat wordt niveaurij genoemd. Laten we zeggen dat we in een labyrint met diepte van 4 het pad eerst langs het 3de niveau gaat, dan langs het 2de hierna langs het 1ste om te eindigen bij het 4de niveau dan zal deze labyrint volgende niveaurij hebben: 0-3-2-1-4. De niveaurij van een labyrint bepaald de structuur. Labyrinten met even veel wendingen en niveaus kunnen toch een heel verschillende structuur hebben.

Niveaurijen van labyrinten zijn (n+1)! permutaties.

Enkelvoudig Alternerend Labyrint[bewerken]

Om te verduidelijken wat een EAL (enkelvoudig alternerend labyrint) net is moeten we zijn structuur definiëren. Zoals we hebben gezien wordt de structuur van een labyrint vooral gedefinieerd door zijn niveaurij(en). Dus laten we even de definitie van een EAL onder de loop nemen

Enkelvoudige: Hierbij is het belangrijk dat de niveaurij altijd begint met niveau 0 en eindigt met het niveau waar het doel d zich bevindt.
Alternerende: Dit betekent dat het pad regelmatig van doorlooprichting moet veranderen. Hierbij moeten in de niveaurijen van EAL's de even en oneven getallen elkaar altijd afwisselen.
Labyrint: Dit bestaat uit 1 pad die zich niet mag snijden. Als men dan segmenten neemt van de niveaurijen moet er een even en oneven getal zijn per segment.

We noemen deze eisen de E, A en L eisen.

Aantal enkelvoudige niveaurijen met diepte "d"[bewerken]

Het aantal labyrinten dat aan de E-eis voldoen kan worden opgelost met de permutatie (n+1)! waarbij het nulste niveau en het doel niet bij "n" horen. Dus bij een labyrint met diepte 5 zullen er 1×2×3×4 = 24 mogelijke combinaties niveaurijen zijn die aan de E-eis zullen voldoen.

De A-eis[bewerken]

Om ervoor te zorgen dat een labyrint windingen maakt zonder dat het pad zich snijdt, moet het pad afwisselend langs even en oneven niveaurijen gaan. Een labyrint met niveaurij 0-2-1-3-4 zal dus zijn eigen pad snijden omdat het pad langs twee oneven niveaus na elkaar gaat. Het Kretalabyrint voldoet aan de A-eis omdat in zijn niveaurij even en oneven getallen elkaar afwisselen.

De L-eis[bewerken]

De L-eis kan enkel visueel worden weergegeven. Het houdt vooral in om labyrinten die voldoen aan de A-eis en E-eis te teken om te zien of het pad zeker niet snijdt. Dat is een heel belangrijke eis omdat niet elke Enkelvoudige Alternerend pad een labyrint is. Een niveaurij van 0-3-4-1-2-5 voldoet zowel aan de E-eis als aan de A-eis toch is het wiskundig onmogelijk om daar een labyrint van te maken omdat deze zich snijdt.

Constructie[bewerken]

Een EAL maken, vergt creativiteit en inzicht. We beginnen bij de constructie van het klassieke labyrint en die gaat als volgt. Bij het ontwerpen van een labyrint is het het makkelijkste om bij de kern te beginnen en in het geval van de klassieke constructie is de kern opgebouwd uit een kruis met 4 winkelhaken en 4 stippen: dit noemen we het zaadpatroon. Daarna worden twee naburige winkelhaken met elkaar verbonden en 2 stippen met andere 2 ander winkelhaken verbonden.